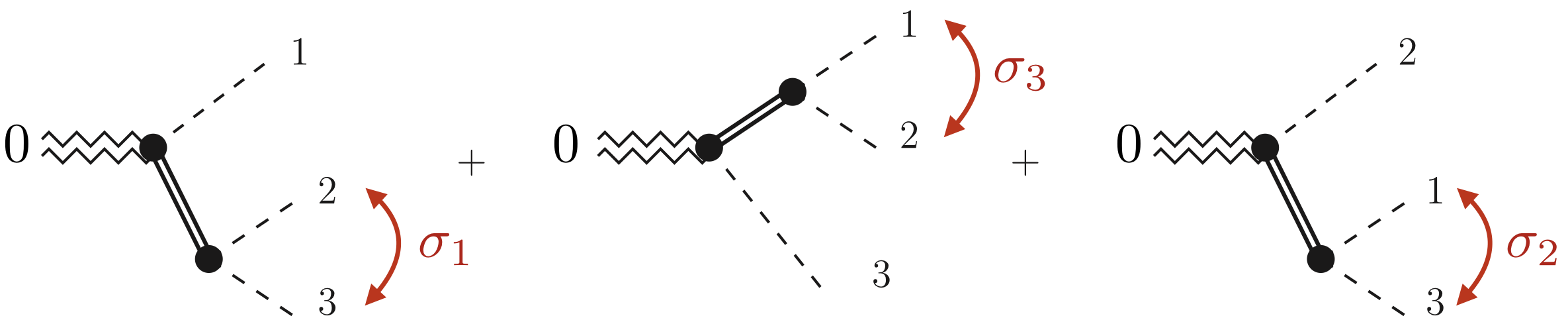
This page concerns any three-body decay parametrized in terms of two-body isobars, as depicted in the figure below.
The details have been presented in the publication [Mik19b].
The code, available in the resources section, returns the recoupling coefficients.
The section notation provides the definition of the angles and helicities appearing in the
recoupling coefficients .
Recoupling Coefficients
The decaying particle ($0$) might be polarized and that polarization depends in the particular experiment.
In the particle $0$ rest frame, the momenta of the particles $1,2,3$ form the $xz$ plane
(defined in the next section), whose orientation in the lab frame frame is given by Euler angles
(to be determined for each event):
\begin{align} \label{eq:master}
M_{\Lambda_\text{Lab}, \{ \lambda^* \}}(\sigma_1, \sigma_2) & =
\sum_{\Lambda^*} D^{J_0*}_{\Lambda_\text{Lab},\Lambda^*} (\alpha,\beta, \gamma) O_{\Lambda^*, \{ \lambda^* \}}
(\sigma_1, \sigma_2).
\end{align}
We used the collective notation $ \{ \lambda^* \} = \{ \lambda^*_1, \lambda^*_2, \lambda^*_3 \}$.
The $D^{J_0*}_{\Lambda_\text{Lab},\Lambda^*} (\alpha,\beta, \gamma)$ in \eqref{eq:master}, is relevant
only if the particle $0$ is polarized. In this case the intensity reads
\begin{align}
\frac{d \sigma}{d \Phi_3} & = N \sum_{\Lambda_\text{Lab},\Lambda'_\text{Lab} }
\rho_{\Lambda_\text{Lab}, \Lambda'_\text{Lab}}
\sum_{\Lambda^*,\Lambda^{*'} }
D^{J_0*}_{\Lambda_\text{Lab},\Lambda^*} D^{J_0}_{\Lambda'_\text{Lab},\Lambda^{*'}}
\sum_{\{\lambda^*\},\{ \lambda^{*'}\} } O_{\Lambda^*, \{ \lambda^* \}} O^*_{\Lambda^{*'}, \{ \lambda^{*'} \}} \\
& \overset{\text{unpolarized}}{\rightarrow}
N \sum_{\Lambda^*, \{\lambda^*\} } \left| O_{\Lambda^*, \{ \lambda^* \}} \right|^2.
\end{align}
The Dalitz plot function $O_{\Lambda^*, \{ \lambda^* \}}(\sigma_1, \sigma_2)$ is written as a sum of three terms,
each corresponds to an isobar chain:
\begin{align}
O_{\Lambda^*, \{ \lambda^* \}} (\sigma_1, \sigma_2) & =
O^1_{\Lambda^*, \{ \lambda^* \}} (\sigma_1, \sigma_2)
+ O^2_{\Lambda^*, \{ \lambda^* \}} (\sigma_1, \sigma_2)
+ O^3_{\Lambda^*, \{ \lambda^* \}}(\sigma_1, \sigma_2).
\end{align}
Each isobar chain $O^k$ involves an isobar line-shape function $H^{s_k\to i+j}_{\lambda_i,\lambda_j}(\sigma_k)$,
a function $H^{0\to (ij)+k}_{\Lambda_k,\lambda_k^*}(m_0^2)$ describing the decay of particle $0$
to the isobar $k$ and the particle $k$
and a recoupling coefficient $C^{s_k, \Lambda_k}_{\Lambda, \{\lambda^*\}, \{\lambda\}}$:
\begin{align}
O^k_{\Lambda^*, \{\lambda^*\}} & = \sum_{s_k, \Lambda_k,\{\lambda\}}
C^{s_k, \Lambda_k}_{\Lambda, \{\lambda^*\}, \{\lambda\}}
H^{0\to (ij)+k}_{\Lambda_k,\lambda_k^*}(m_0^2)
H^{s_k\to i+j}_{\lambda_i,\lambda_j}(\sigma_k)
\end{align}
The recoupling coefficients depend only of the kinematics and the spin of the external particles:
\begin{align}
C^{s_k, \Lambda_k}_{\Lambda, \{\lambda^*\}, \{\lambda\}}(\sigma_1,\sigma_2) & =
d^{J_0}_{\Lambda^*, \Lambda_k-\lambda_k^*}(\theta^*_{k1}) d^{s_k}_{\Lambda_k,\lambda_i-\lambda_j}(\theta_{ij}) \times d^{J_i}_{\lambda_i,\lambda_i^*}(-\omega_{i|k}) d^{J_j}_{\lambda_j,\lambda_j^*}(\omega_{j|k})
\end{align}
The first two Wigner-$d$ functions originate from the two decays and
the last two from the Wigner rotation implied by the boost from the isobar rest frame to
the particle $0$ rest frame.
The code returns the recoupling coefficients $C^{s_k, \Lambda_k}_{\Lambda, \{\lambda^*\}, \{\lambda\}}(\sigma_1,\sigma_2)$.
Notations
 Let us consider the three-body decay
\begin{align}
0(\Lambda, p_0) \to 1 (\lambda_1, p_1) + 2 (\lambda_2, p_2) +3 (\lambda_3, p_3).
\end{align}
Let us call $m_i$ and $J_i$ the mass and spin of particle $i=0,1,2,3$.
Let us consider the three-body decay
\begin{align}
0(\Lambda, p_0) \to 1 (\lambda_1, p_1) + 2 (\lambda_2, p_2) +3 (\lambda_3, p_3).
\end{align}
Let us call $m_i$ and $J_i$ the mass and spin of particle $i=0,1,2,3$.
$\{i,j,k\}$ form a permutation of 123 and $\sigma_k = (p_i+p_j)^2$.
The Mandelstam variables obey $\sigma_1+\sigma_2 + \sigma_3 = m_0^2 + m_1^2+m_2^2+m_3^2$.
The isobar $1$ means the isobar formed by particle 2 and 3, etc.
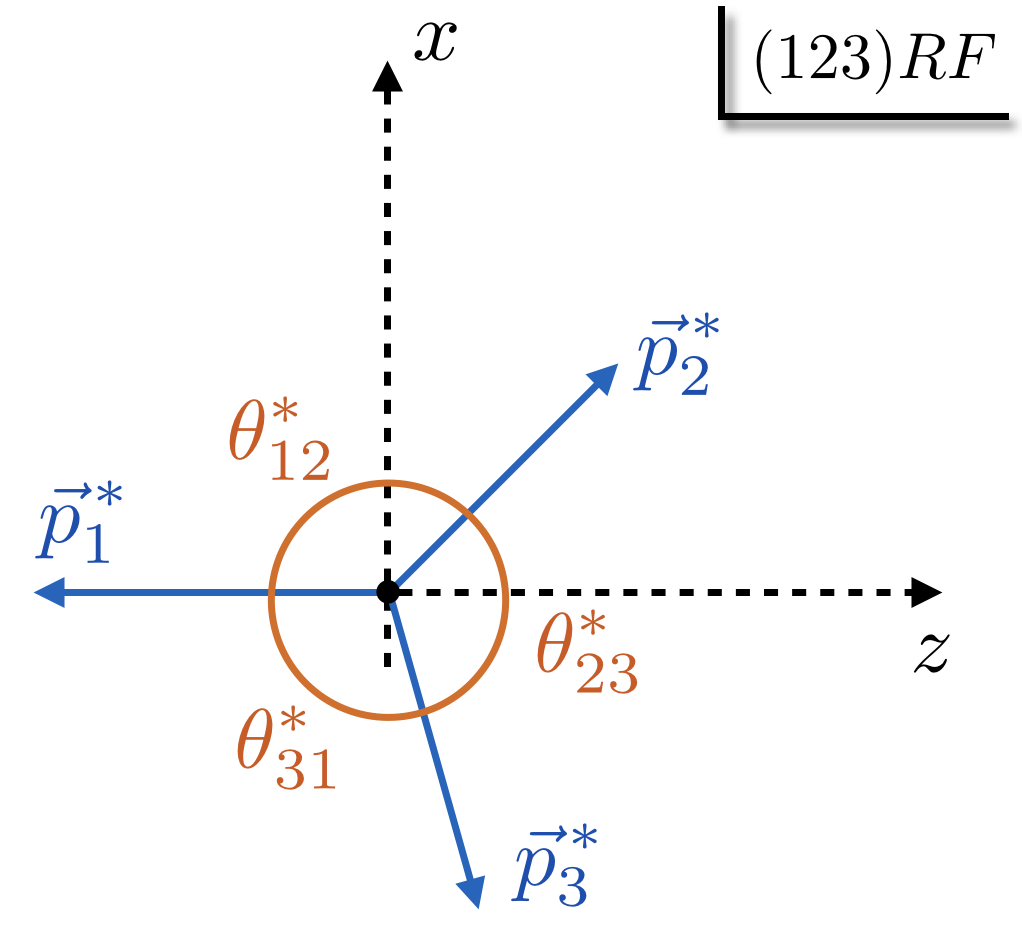
In the center-of-momentum of particle 0 (CMF),
the vector $\vec{ p}_1^{\, *}$, $\vec{ p}_2^{\, *}$ and $\vec{ p}_3^{\,*}$ form a plane, the decay plane.
All quantities in the CMF are denoted with a $^*$.
The CMF is also called the (123)RF, or the (123) Rest Frame.
The decay plane is the $xz$ plane with the $z$ axis being the opposite direction of $\vec{ p}_1^{\, *}$ in the CMF
and the $y$ axis being the opposite direction of $\vec{ p}_1^{\, *} \times \vec{ p}_2^{\, *}$ in the CMF.
In the CMF, $\theta_{ij}^*$ is the angle between $\vec{ p}_i^{\, *}$ and $\vec{ p}_j^{\, *}$.
Thus $\theta^*_{k1}$ is the angle between the isobar $k$ ($-\vec{ p}_k^{\, *}$) and the $z$ axis ($-\vec{ p}_1^{\, *}$).
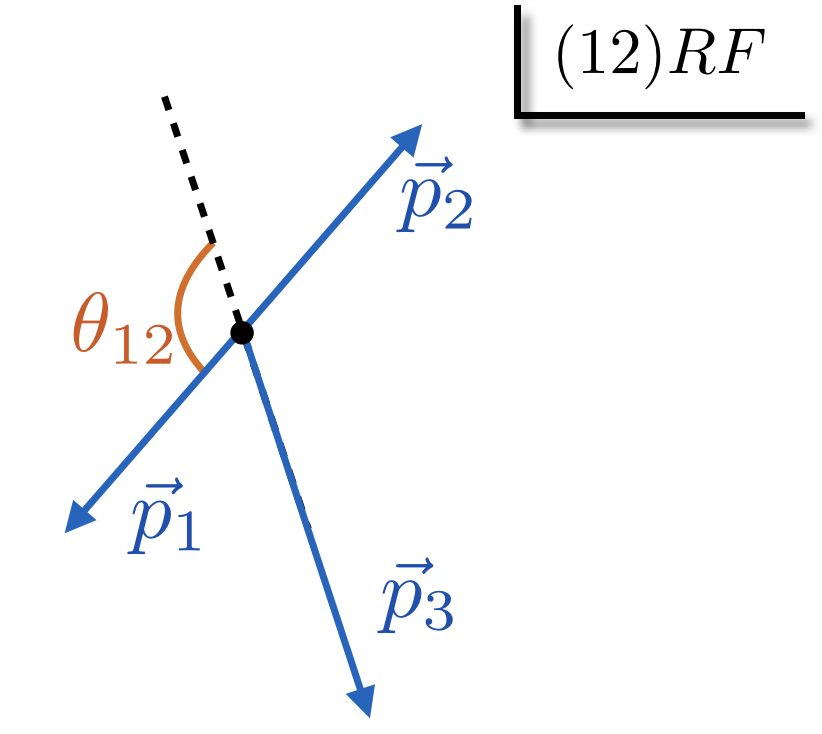
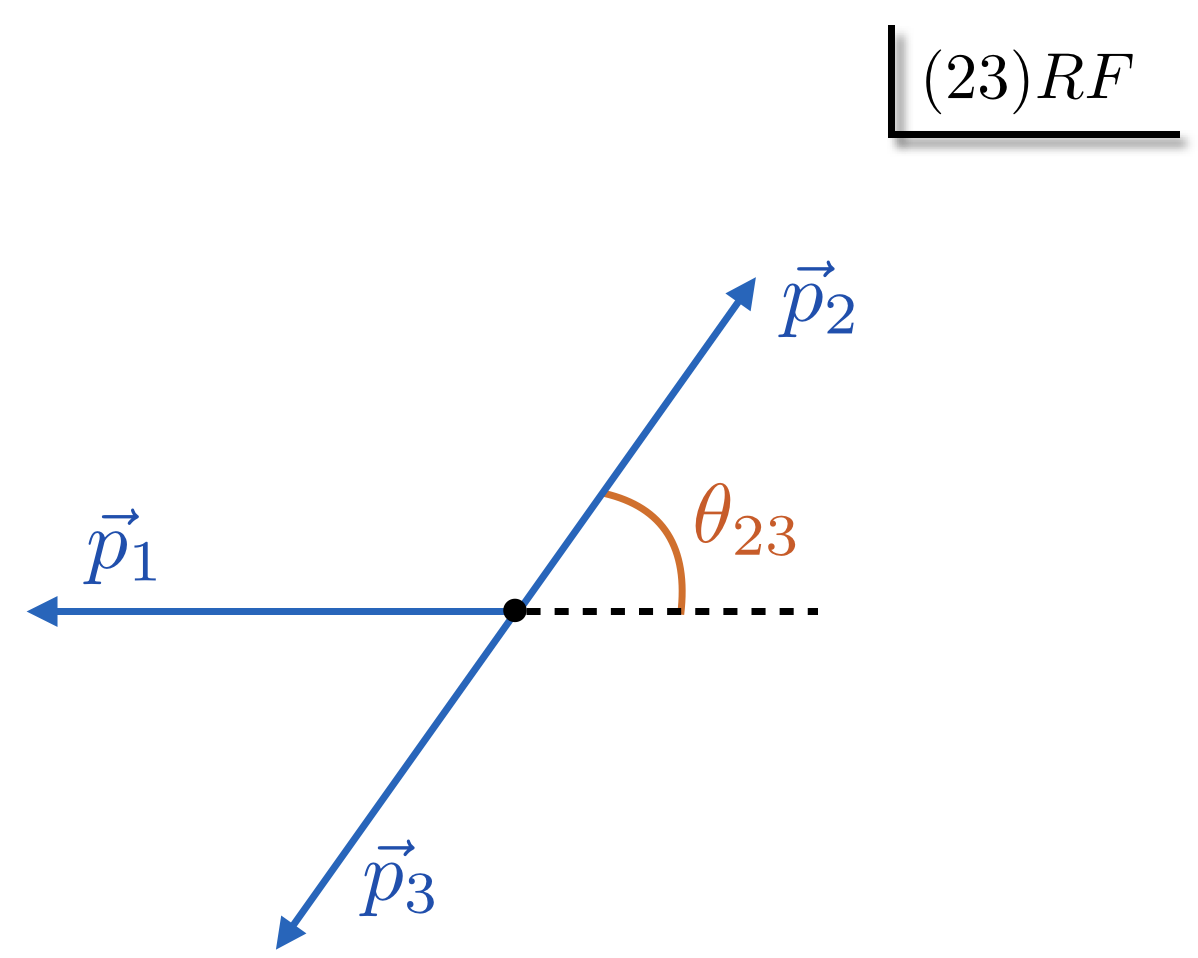
The rest frame of particles $ij$ is called the $(ij)$RF.
In the $(ij)$RF, the scattering angle $\theta_{ij}$ is the angle between $\vec p_i$ and $-\vec p_k$
is called $\theta_{ij}$.
The three isobar rest frames are illustrated on the figures:
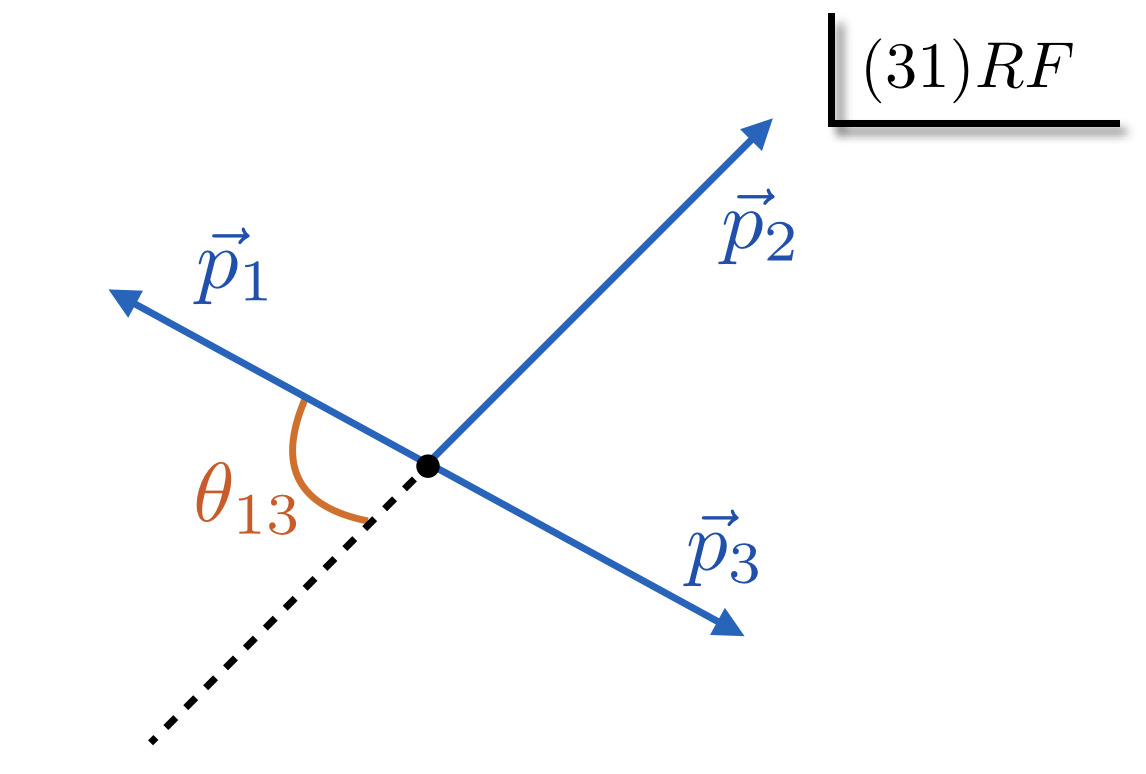
We will also need the angles corresponding to the Wigner rotations
induced by the boosting from an isobar frame to the CMF.
$\omega_{i|k}$ is the angle of the Wigner rotation bringing particle $i$ from the isobar $k$ rest frame to the CMF.
One can shown that $\omega_{j|k}$ is positive when $ijk$ are even permutation of $123$.
Since the angles are specified by their cosine, we need to take the sign into account.
The expressions of the cosine of the angles in term of Mandelstam variables are
\begin{align}
\cos \theta^*_{ij} & = \frac{(m_0^2+m_i^2-\sigma_i)(m_0^2+m_j^2-\sigma_j)+ 2m_0^2(m_i^2+m_j^2-\sigma_k)}
{\lambda^{1/2}(m_0^2, m_i^2,\sigma_i) \lambda^{1/2}(m_0^2, m_j^2,\sigma_j)} \\
%
\cos \theta_{ij} & =- \frac{\sigma_k(\sigma_i-\sigma_j) + (m_i^2-m_j^2)(m_0^2-m^2_k)}
{\lambda^{1/2}(\sigma_k, m_i^2, m_j^2) \lambda^{1/2}(m_0^2, m_k^2,\sigma_k)} \\
%
\cos \omega_{i|k} & = \frac{(\sigma_k+m_i^2-m_j^2)(m_0^2+m_i^2-\sigma_i)- 2m_i^2(\sigma_k-m_k^2+m_0^2)}
{\lambda^{1/2}(\sigma_k, m_i^2,m_j^2) \lambda^{1/2}(m_0^2, m_i^2,\sigma_i)}
\end{align}
The triangle function is $\lambda(a,b,c) = a^2 + b^2 + c^2 - 2(a b + b c + ca)$.
Every amplitude is a function of any two Madelstam variables $\sigma_1,\sigma_2,\sigma_3$
and helicities/spin projection.
Helicities (and spin projections) notations:
- $\lambda_{i}^*$ are the helicities of particle $i=1,2,3$ in the (123)RF.
- $\Lambda^*$ is the spin projection of particle 0 along the $z$ axis in the (123)RF.
- $\lambda_{i}$ are the helicities of particle $i=0,1,2,3$ in the isobar $(ij)$RF.
- $\Lambda_k$ is the spin projection along $-\vec p_k$ of the isobar $(ij)$ in its RF. $\Lambda_k$ is also the helicity of the isobar in the (123)RF.
- $s_k$ is the spin of the isobar $(ij)$.
Examples
As in the publication [Mik19b], the code illustrates the formalism on the three examples.
For each example, we include one isobar in each channel.
| | | isobar $1$ | isobar $2$ | isobar $3$ | ||
| $A:$ | $\Lambda_c(0) \to p(1) K(2) \pi(3)$ | | | $K^* \ 1^{-}$ | $\Delta\ \frac{3}{2}^+$ | $\Lambda\ \frac{3}{2}^-$ |
| $B:$ | $B_0(0) \to \psi(1) \pi(2) K(3)$ | | | $K^* \ 1^-$ | nothing | $Z\ 1^-$ |
| $C:$ | $\Lambda_b(0) \to p(1) K(2) J/\psi(3)$ | | | nothing | Pentaquark $\frac{3}{2}^+$ | $\Lambda\ \frac{1}{2}^+$ |
These examples are already predefined in the code for illustration but the functions can be applied for any reaction with any isobar.
References
[Mik19b]
M. Mikhasenko, et al (JPAC),
``Dalitz-plot decomposition for three-body decays,''
arXiv:1910.04566 [hep-ph],
V. Mathieu, summarizing note.
Resources
- Julia implementation on GitHub.
- C/C++: All C/C++ files in a .zip, link to the GitHub repository.
- Contact person: Vincent Mathieu
- Last update: January 2019
To compile: gcc main.cpp Dalitz-couplings.cpp
main.cpp computes the recouplings coefficients for a chosen example in a grid within the Dalitz boundaries.
- recoupling_coef:
Compute the recoupling coefficients.
Inputs:- int k = #chain
- double sk = isobar spin
- double IsoHel[4] = helicities of {0,1,2,3} in the isobar rest frame
- double CMFhel[4] = heliciticies of {0,1,2,3} in the CMF
- double spin[4] = spin of the particles {0,1,2,3}
- double mass2[4] = squared masses of particles {0,1,2,3}
- double inv[4] = $\sigma_{1,2,3}$. The index 0 is not used.
- cos_center_of_mass_angle: Compute $\cos \theta^*_{ij}$.
- cos_isobar_frame_angle: Compute $\cos \theta_{ij}$.
- cos_wigner_angle: Compute $\cos \omega_{i|j}$.

