 We present the model published in [Mat18a]
concerning the spin density matrix elements of light neutral vector meson ($\omega$, $\rho^0$, $\phi$) photoproduction.
We present the model published in [Mat18a]
concerning the spin density matrix elements of light neutral vector meson ($\omega$, $\rho^0$, $\phi$) photoproduction.
We report here only the main features of the model.
The code can be downloaded in Resources section and simulated
in the Simulation section.
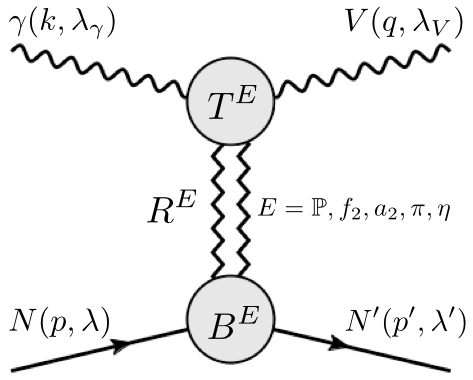
Our model for the helicity amplitudes of vector meson photoproduction involves the $\pi$ and $\eta$ meson unnatural exchanges,
Pomeron, $f_2$ and $a_2$ natural exchanges:
\begin{align}
{\cal M}_{\substack{\lambda_V, \lambda_\gamma \\ \lambda', \lambda}}(s,t) & =
\sum_{E = \pi,\eta, {\mathbb P}, f_2, a_2}
{\cal M}^{E}_{\substack{\lambda_V, \lambda_\gamma \\ \lambda', \lambda}}(s,t).
\end{align}
The helicities are defined in the center-of-mass frame of the reaction
$\gamma(k,\lambda_\gamma) N(p,\lambda)\to V(q,\lambda_V) N'(p',\lambda')$.
The Mandelstam variables are $s = (k+p)^2$ and $t = (k-q)^2$.
At high energy, the amplitudes for the $\pi$ and $\eta$ meson exchange reads
\begin{align} \label{eq:pion}
{\cal M}^P_{\substack{\lambda_V, \lambda_\gamma \\ \lambda', \lambda}}(s,t) & =
\beta^P_0 \lambda_\gamma \delta_{\lambda,-\lambda'} \sqrt{-t} \left[
\delta_{\lambda_\omega,\lambda_\gamma}
- \sqrt{2} \lambda_\gamma \frac{ \sqrt{-t} }{m_V}\delta_{\lambda_\omega,0}+
\frac{-t}{m_V^2} \delta_{\lambda_\omega,-\lambda_\gamma} \right]
\frac{1+e^{-i\pi\alpha_\pi(t)}}{2 \sin \alpha_\pi(t)}\left(\frac{s}{s_0} \right)^{\alpha_\pi(t)}
\end{align}
with $\beta^P_0 = -m_V^2 \pi \alpha_1 g_{V P\gamma}g_{P NN}e^{b_P t}/2$ and $P = \pi, \eta$.
We will assume factorization into a top and a bottom vertex together with a Regge factor:
\begin{align} \label{eq:naturalM}
{\cal M}^R_{\substack{\lambda_V, \lambda_\gamma \\ \lambda', \lambda}}(s,t)
& = \beta_R^{\gamma V} e^{b_Rt} \ V^{\gamma V}_{\lambda_V \lambda_\gamma}(t) R(s,t) V^{pp}_{\lambda' \lambda}(t).
\end{align}
The helicity structure at the photon vertex is:
\begin{align} \label{eq:topV}
V^{\gamma V}_{\lambda_V \lambda_\gamma}(t) & = \lambda_\gamma^2 \left(\delta_{\lambda_V,\lambda_\gamma} + \beta^R_1 \frac{\sqrt{-t}}{m_V}
\frac{\lambda_\gamma}{\sqrt{2}} \delta_{\lambda_V,0} +\beta^R_2
\frac{-t}{m^2_V} \delta^{\lambda_V,-\lambda_\gamma} \right).
\end{align}
The helicity structure at the nucleon vertex is:
\begin{align}
V^{pp}_{\lambda' \lambda}(t) & = \delta_{\lambda,\lambda'} + 2 \lambda \kappa_R \frac{\sqrt{-t}}{2m} \delta_{\lambda,-\lambda'}.
\end{align}
The Regge factor is, with the trajectory $\alpha(t) = \alpha_0 + \alpha_1 t$:
\begin{align}
R(s,t) & = \frac{\alpha_R(t)}{\alpha_R(0)} \frac{1+e^{-i\pi\alpha_t(t)}}{\sin\pi\alpha_R(t)} \left(\frac{s}{s_0}\right)^{\alpha_R(t)}.
\end{align}
The spin density matrix elements (SDME) computed in the $s$-channel frame are equivallent to the
SDME in the helicity frame.
The relation between the helicity frame and the Gottfried-Jackson frame is
\begin{align}
\rho^i_{MM'}|_{GJ} & = \sum_{\lambda \lambda'} d^1_{M\lambda}(\theta) \rho^i_{\lambda \lambda'}|_{H} d^1_{M'\lambda'}(\theta)
\end{align}
The definition of the SDME $\rho^i_{MM'}$ and the frames are given in Ref. [Mat17a] .
At high energy, the rotation angle $\theta$ is simply
\begin{align}
\cos\theta & = \frac{m_V^2+t}{m_V^2-t}.
\end{align}
The code uses the leading $s$ expression for the rotatio angles to be consistent with the helicity amplitudes.
One can check that with only the unnatural exchanges (set the natural exchanges couplings to 0),
the SDME in the Gottfried-Jackson frame take the simple form $\rho^0_{00} = \text{Re }\rho^0_{10}= \rho^0_{1-1}=0$.
The parameters are determined on the SLAC data Ref. [Bal73] . We refer to the publication [Mat17a] for the procedure. In the Simulation section, the default values of the parameters are listed in Table. The scale factor in the Regge factor is set to $s_0 = 1$ GeV$^2$.
| $\mathbb P$ | $f_2$ | $a_2$ | | | $\pi$ | $\eta$ | ||
| $\beta^{\gamma \omega}$ | 0.739 | 0.730 | 1.256 | | | $g_{\omega P \gamma }$ | 0.696 | 0.479 |
| $\beta^{\gamma \rho}$ | 2.506 | 2.476 | 0.370 | | | $g_{\rho P \gamma }$ | 0.252 | 0.136 |
| $\beta^{\gamma \phi}$ | 0.932 | 0.000 | 0.000 | | | $g_{\phi P \gamma }$ | 0.040 | 0.210 |
| $b$ | 3.6 | 0.55 | 0.53 | | | $b $ | 0.0 | 0.0 |
| $\beta_1$ | 0.00 | 0.95 | 0.83 | | | $g_{P NN }$ | 13.26 | 2.24 |
| $\beta_2$ | 0.00 | $-$0.56 | 0.00 | | | |||
| $\kappa$ | 0.0 | 0.0 | 8.0 | | | |||
| $\alpha_0$ | 1.08 | 0.5 | 0.5 | | | $\alpha_0$ | $-0.013$ | $-0.013$ |
| $\alpha_1$ | 0.2 | 0.9 | 0.9 | | | $\alpha_1$ | $0.7$ | $0.7$ |
They correspond to the values determined in the publication [Mat18a] .
References
[Mat18a]
V. Mathieu, et al (JPAC),
``Vector Meson Photoproduction with Linearly Polarized Beam,''
arXiv:1802.09403 [hep-ph],
[Bal73]
Ballam, et al (SLAC),
``Vector Meson Production by Polarized Photons at 2.8 GeV, 4.7 GeV, and 9.3 GeV,''
Phys. Rev. D 7, 3150 (1973)
Resources
- Publications: [Mat17a]
- C/C++: C/C++ file
- Input file: param.txt , simu.txt .
- Output files: resultsH.txt , resultsGJ.txt
- gnuplot files: gnuplotH.txt , gnuplotGJ.txt
- Contact person: Vincent Mathieu
- Last update: December 2017
- param.txt:
The 3 first lines are the parameters for the Pomeron, f2 and a2 exchange respectively
Each of these 3 lines is in the format:$\alpha_0$ $\alpha_1$ $b$ $\beta^{\gamma V}$ $\beta_1$ $\beta_2$ $\kappa$
The next 2 lines corresponds to the $\pi$ and $\eta$ exhchanges.
Each of these 3 lines is in the format:$\alpha_0$ $\alpha_1$ $b$ $g_{V P\gamma }$ $g_{P NN}$
- simu.txt:
The format of this file is:$V$ $E_g$ $t_0$ $t_1$ $dt$
The grid in $t$ is from $t_1$ to $t_0$ by step of $dt$.
To faciliate the display of the results the $t$ range is fixed in the online simulation.
The parameters are, in GeV$^2$, $t_1 = -1$, $t_0 = 0$ and $dt = 0.05$.
The code can be run with a different $t$ range.
- resultsH.txt and resultsGJ.txt:
The results of the simulations in the helicity and Gottfried-Jackson frames.
The first column is $-t$ in GeV$^2$. The following 9 columns are$\rho^0_{00}$ Re $\rho^0_{10}$ $\rho^0_{1-1}$ $\rho^1_{11}$ $\rho^1_{00}$ Re $\rho^1_{10}$ $\rho^1_{1-1}$ Im $\rho^2_{10}$ $\rho^2_{1-1}$
- amplvector:
Compute the helicity amplitudes of the complete model.
It sums over the Pomeron, $f_2$, $a_2$, $\pi$ and $\eta$ exchanges. - amplNat:
Compute the helicity amplitudes of one natural exchange.
Only the photon and nucleon vertices are returned.
The Regge factor and the overall normalization are added in the function amplvector. - amplPi:
Compute the helicity amplitudes of one pseudoscalar exchange.
Only the photon and nucleon vertices are returned.
The Regge factor and the overall normalization are added in the function amplvector. - sdmeNorm:
compute the norm of the SDME: \begin{align*} \sum_{\lambda_\gamma,\lambda_V,\lambda,\lambda'} \left| {\cal M}_{\substack{\lambda_V, \lambda_\gamma \\ \lambda', \lambda}}(s,t) \right|^2 \end{align*} - sdmeH:
compute the SDME in the helicity frame. - sdmeGJ:
compute the SDME in the Gottfried-Jackson frame.
The SDME are computed in the helicity frame and rotated to the Gottfried-Jackson frame.

