This page concerns the Finite Energy Sum Rules for pion-nucleon scatterings from the publication [Mat15b] .
A brief description of the formalism is given in the Formalisms section.
Please refer to the $\pi N$ page or the publication [Mat15b] for further details.
Both side of the sum rules are compared interactively in Simulation section. The user can also submit its partial waves.
The code can be downloaded in Resources section.

Formalism

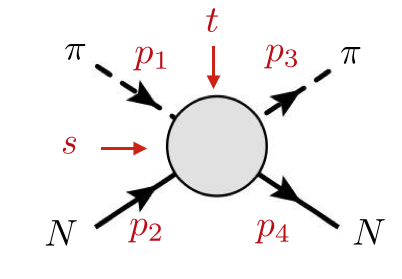The pion-nucleon scattering is a function of 2 variables. We are using the the momentum transfered squared $t$ (in GeV$^2$) and the crossing variable $\nu$ defined by \begin{align} \nu = \frac{s-u}{4M} = E_\text{lab} + \frac{t}{4M}. \end{align} The pion mass is $\mu$ and the proton mass is $M$.

The scattering amplitude $\left(T_{\lambda_2 \lambda_4} \right)_{ji}^{ba}$ for the reaction $\pi^a N_i \to \pi^b N_j$ is decomposed into scalar amplitudes. Assuming isospin symmetry, we can attach to each scalar amplitude an isospin index: \begin{align} \left(T_{\lambda_2\lambda_4}\right)_{ji}^{ba} & = \bar u(p_4,\lambda_4) \left[ A_{ji}^{ba} + \frac{1}{2} (p_1\!\!\!\!\! /\ +p_3\!\!\!\!\! / \ ) B_{ji}^{ba} \right] u(p_2,\lambda_2). \label{eq:T} \\ A_{ji}^{ba} & = \delta_{ji}\delta^{ba} A^{(+)} + i \epsilon_{bac}(\tau^c)_{ji}A^{(-)} \end{align} The indices $(a,b)$ and $(i,j)$ are isospin indices for $I=1$ (pion) and $I=\frac{1}{2}$ (nucleon).
It is often convenient to define another scalar amplitudes denoted by $C$ or $A'$ \begin{align} C \equiv A' \equiv A + \frac{M(s-u)}{4M^2-t} B = A + \frac{\nu}{1-t/4M^2} B. \end{align}

In the following we will only consider the amplitudes $\nu B^{(\pm)}$ and $A'^{(\pm)}$.
The have good quantum number in the $t$-channel $\pi\pi \to N \bar N$. $A'$ (B) is helicity non-flip (helicity flip) in the $t-$channel.
We denote these quantum numbers by name of the lowest spin particle in the Regge trajectory. They are \begin{align*} \nu B^{(-)}&: & \rho & & \text{odd:} &&(-\nu)B^{(-)}(-\nu,t) &= - \nu B^{(-)}(\nu,t) \\ A'^{(-)}&: & \rho & & \text{odd:} &&A'^{(-)}(-\nu,t) &= -A'^{(-)}(\nu,t) \\ \nu B^{(-)}&: & f_2 + \mathbb P & & \text{even:} && (-\nu)B^{(-)}(-\nu,t) &= + \nu B^{(-)}(\nu,t) \\ A'^{(-)}&: & f_2 + \mathbb P & & \text{even:} && A'^{(-)}(-\nu,t) &= +A'^{(-)}(\nu,t) \\ \end{align*} We have also indicated their crossing properties under the change $\nu \to -\nu$.

If, for an amplitude $F = A'^{(\pm)}, \nu B^{(\pm)}$, we assume one Regge pole of the form: \begin{align} \text{Im } R(\nu,t) = \beta(t) \nu^{\alpha(t)} \end{align} the finite energy sum rules are \begin{align} \kappa_F \pi \nu_B\frac{g^2}{2M}\left(\frac{\nu_B}{\Lambda}\right)^k + \frac{1}{\Lambda^k} \int_{\nu_0}^{\Lambda} \text{Im } F(\nu,t) \nu^k d \nu = \frac{\beta(t)\Lambda^{\alpha(t)+1}}{\alpha(t)+k+1} \label{eq:FESR} \end{align} The moment $k$ is odd (even) for an even (odd) amplitudes.
In the even amplitudes $F^{(+)}$, they are two term in the RHS of the sum rules Eq. \eqref{eq:FESR}:
one for the $f_2$ Regge pole and one for the Pomeron.
The pion-nucleon coupling, nucleon pole, thresold and cutoff are \begin{align} g^2 &= 56\pi, & \nu_B &= \frac{t-2\mu^2}{4M}, & \nu_0 &= \mu + \frac{t}{4M}, & \Lambda & = E_\text{lab}^\text{max} + \frac{t}{4M} \end{align} For $F = \nu B$, we have $\kappa_F = 1$,
For $F = A'$, we have $\kappa_F = 1/(1-t/4M^2)$.
The sum rules are dimensionless but will be expressed in mb.GeV$^2$ thanks to $1 = \hbar^2 = 0.389352$ mb.GeV$^2$.

Model

At high energy $p_\text{lab}>2.5$ GeV, we use a Regge parametrization for the invariant amplitudes.
The $t-$channel isospin-1 amplitudes involve a $\rho$ Regge pole: \begin{align} \nonumber \text{Im }A'^{(-)} &= -C^\rho_0\left[(1+C^\rho_2)e^{C^\rho_1 t}-C^\rho_2\right] \frac{\pi \nu^{\alpha_\rho}}{2 \Gamma(\alpha_\rho+1)} , \\ \text{Im }\nu B^{(-)} &= D^\rho_0 e^{D^\rho_1 t} \frac{\pi \nu^{\alpha_\rho}}{2\Gamma(\alpha_\rho)}. \end{align}

The $t-$channel isospin-0 amplitudes involve the Pomeron pole and a $f$ Regge pole: \begin{align} A'^{(+)} & = A'^{\mathbb P} + A'^f & B^{(+)} & = B^{\mathbb P} + B^f \end{align} The Regge parametrization for these poles are given by \begin{align} \nonumber \text{Im } A'^{\mathbb P} &= C_0^{\mathbb P}e^{C_1^{\mathbb P} t} \frac{\pi \nu^{\alpha_{\mathbb P}}}{2\Gamma(\alpha_{\mathbb P})} , & \nu B^{\mathbb P} &= A'^{\mathbb P},\\ \text{Im } A'^f &= C_0^fe^{C_1^f t}\frac{\pi \nu^{\alpha_f}}{2\Gamma(\alpha_f)}, & \nu B^f &= A'^f. \end{align} In the Regge parametrization, the crossing variable $\nu$ is expressed in GeV.
The trajectories $\alpha(t) = \alpha(0) + \alpha' t + \alpha'' t^2$ are at most quadratic in $t$.
The contribution of the $f_2$ and Pomeron poles add in the FESR Eq. \eqref{eq:FESR}.
The trajectories and the other parameters are given in the Table I of [Mat15b] .
In the Simulation section, the user can change these values.
The range of validity of the Regge parametrization is $t\in [-1,0]$ GeV$^2$ and $p_\text{lab}>2.5$ GeV.
However the formula are analytic in $t$ and can be extended for $t< -1$ GeV$^2$.

The left-hand side (LHS) of the sum rules can be computed from any low energy model given in term of partial waves.
Below the user could generate the LHS of the FESR with the models from the references:
[Wor12a] , [Ani12a] , [Ron13a] , [KH80] , [ANL-O] .

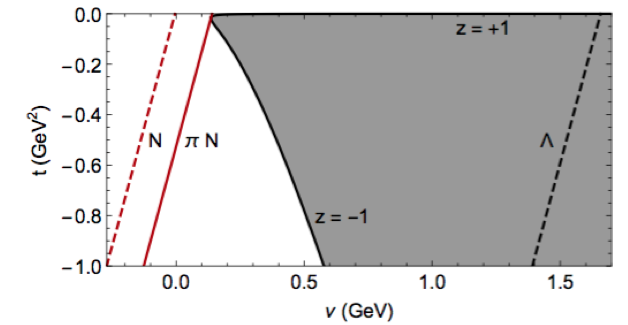The integration in the FESR Eq. \eqref{eq:FESR} is performed at fixed $t$.
For $t\neq 0$, the integral involve a unphysical region.
The physical region ($|z = \cos\theta| \le 1$) is the grey area in the figure.
The solid (dashed) red line represent the $\pi N$ threshold (nucleon pole).
The extrapolation outside the physical region is performed by evaluating the Legendre polynomials for $\cos\theta \le -1$.
High partial wave might compromise the numerical stability of the amplitudes in the unphysical region.
For this reason, we limit the number of waves to $L_\text{max} = 6$ for the models in the resonance region.

References

[Mat15b]
V. Mathieu, I. V. Danilkin, C. Fernandez-Ramirez, M. R. Pennington, D. Schott, A. P. Szczepaniak and G. Fox
``Toward Complete Pion Nucleon Amplitudes,'' arXiv:1506.01764 [hep-ph], Phys. Rev. D 92, 074004 (2015)

[Wor12a]
R.L. Workman, R.A. Arndt, W.J. Briscoe, M.W. Paris, I.I. Strakovsky
``Parameterization dependence of T matrix poles and eigenphases from a fit to $\pi N$ elastic scattering data,''
arXiv:1204.2277 [hep-ph], Phys. Rev. C 86, 035202 (2012)

[Ani12a]
A.V. Anisovich, R. Beck, E. Klempt, V. A. Nikonov, A. V Sarantsev, U. Thoma
``Pion- and photo-induced transition amplitudes to $\Lambda K, \Sigma K$ and $N\eta$,''
arXiv:1205.2255 [nucl-th], Eur.Phys.J. A48, 88 (2012)

[Ron13a]
D. Ronchen, M. Doring, F. Huang, H. Haberzettl, J. Haidenbauer, C. Hanhart, S. Krewald, U.-G Meissner, K. Nakayama
``Coupled-channel dynamics in the reactions $\pi N \to \pi N, \eta N, K \Lambda, K, \Sigma$,''
arXiv:1211.6998 [nucl-th], Eur.Phys.J. A 49, 44 (2013)

[KH80]
G. Hohler, ed. H. Schopper. 1983. Springer. Landolt-Bornstein Verlag I/9b2
A PDF copy of the book can be provided on demand.

[ANL-O]
H. Kamano, S.X. Nakamura, T. -S. H. Lee, T. Sato
``Nucleon resonances within a dynamical coupled-channels model of $\pi N$ and $\gamma N$ reactions,''
arXiv:1305.4351 [nucl-th], Phys. Rev. C 88, 035209 (2013)

Resources

• Publications: [Mat15a]
• Partial waves: SAID , JuBo , BnGa , KH80 , ANL-O
• C/C++: Main-FESR-PiN.c
• Input file: Regge-param.txt , Simulation-param.txt , Solution.txt
• Output files: output-Bm.txt , output-Bp.txt , output-Cm.txt , output-Cp.txt
• Contact person: Vincent Mathieu (mathieuv.at.indiana.edu)
• Last update: February 2017

Simulation