 We present the model published in [Mat19a]
illustrating the polarized moments for the reaction
\begin{align}
\vec \gamma (p_\gamma) p(p_N) \to \eta(p_\eta) \pi^0(p_\pi) p(p'_N),
\end{align}
with a linearly polarized beam.
The code can be downloaded in Resources section and simulated
in the Simulation section.
We present the model published in [Mat19a]
illustrating the polarized moments for the reaction
\begin{align}
\vec \gamma (p_\gamma) p(p_N) \to \eta(p_\eta) \pi^0(p_\pi) p(p'_N),
\end{align}
with a linearly polarized beam.
The code can be downloaded in Resources section and simulated
in the Simulation section.
Definitions
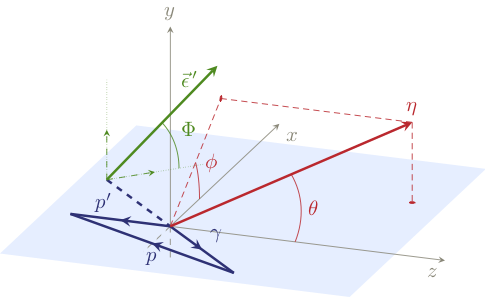
$\Omega = (\theta,\phi)$ are the angles of the $\eta$ in the $\eta\pi$ rest frame. $\Phi$ is the angle between the polarization and the reaction plane. The angles are illustrated on the figure in the helicity frame. The other kinematical variables are the total energy squared $s = (p_\gamma+p_N)^2$, the momentum transferred $t = (p_N- p'_N)^2$ and the $\eta\pi$ mass $m_{\eta\pi}^2 = (p_\eta+p_\pi)^2$.
With a linearly plarized beam, with polarization $P_\gamma$, the intensity is decomposed as \begin{align} I(\Omega,\Phi) & = I^0(\Omega) - P_\gamma I^1(\Omega) \cos 2 \Phi - P_\gamma I^2(\Omega) \sin 2 \Phi. \end{align} The moments are defined by \begin{align} H^0(LM) & =\phantom{- \frac{2}{P_\gamma}} \frac{1}{2\pi}\int I(\Omega,\Phi) d^L_{M0}(\theta) \cos M \phi \ d\Omega d\Phi ,\\ H^1(LM) & = - \frac{2}{P_\gamma}\frac{1}{2\pi}\int I(\Omega,\Phi) d^L_{M0}(\theta) \cos M \phi \cos 2\Phi\ d\Omega d\Phi ,\\ \text{Im }H^2(LM) & = \frac{2}{P_\gamma}\frac{1}{2\pi}\int I(\Omega,\Phi) d^L_{M0}(\theta) \cos M \phi \sin 2 \Phi\ d\Omega d\Phi. \end{align}
The $4\pi$ integrated beam asymmetry $\Sigma_{4\pi}$ and the beam asymmetry along the $y$ axis $\Sigma_y$ are defined by \begin{align} \Sigma_{4\pi} & = \frac{1}{P_\gamma} \frac{\int [I(\Omega,0) - I(\Omega,\frac{\pi}{2})] d\Omega} {\int [I(\Omega,0) + I(\Omega,\frac{\pi}{2})] d\Omega } \\ \Sigma_y & = \frac{1}{P_\gamma} \frac{[I(\Omega_y,0) - I(\Omega_y,\frac{\pi}{2})] } { [I(\Omega_y,0) + I(\Omega_y,\frac{\pi}{2})] }. \end{align} They can be expressed with the moments ($\Sigma_y$ truncated to $L=4$) \begin{align} \Sigma_{4\pi} & = \frac{H^1(00)}{H^0(00)} \\ \Sigma_y & = \frac{H^1(00) - \frac{5}{2} H^1(20) - 5 \sqrt{\frac{3}{2}} H^1(22) + \frac{27}{8} H^1(40) + \frac{9}{2}\sqrt{\frac{5}{2}} H^1(42) + \frac{9}{4}\sqrt{\frac{35}{2}} H^1(44)} {H^0(00) - \frac{5}{2} H^0(20) - 5 \sqrt{\frac{3}{2}} H^0(22) + \frac{27}{8} H^0(40) + \frac{9}{2}\sqrt{\frac{5}{2}} H^0(42) + \frac{9}{4}\sqrt{\frac{35}{2}} H^0(44)} \end{align}
Model
We use the reflectivity basis. Our toy model include only the following waves
\begin{align}
[\ell]^{(\epsilon)}_m = S_0^{(+)}, P_{0,1}^{(+)}, D_{0,1,2}^{(+)}.
\end{align}
$\epsilon$ is the reflectivity of the partial wave.
One can show that $\text{Im }H^2(LM) = -H^1(LM)$ with a basis icluding only waves $[\ell]^{(\epsilon)}_m$
with positive projection $m\ge 0$.
We thus will not display the moments $\text{Im} H^2(LM)$.
The wave are parametrized in the $s$-channel frame by
\begin{align}
[\ell]^{(\epsilon)}_m & = N_0 N_R \left( \delta_R \frac{\sqrt{-t}}{m_R} \right)^{|m-1|}
\frac{m_R \Gamma_R}{m_R^2-m_{\eta\pi}^2-i m_R \Gamma_R}\ \Gamma[1-\alpha(t)](1-e^{-i\pi\alpha(t)}) s^{\alpha(t)}
\end{align}
where $R = a_0(980), \pi_1(1600), a_2(1320), a_2(1700) $ are the resonances in the partial wave $\ell=0,1,2$.
$N_0 = 20000$ is an overal normalization.
The vector trajectory is $\alpha(t) = 0.5 + 0.9t$. $s$ and $t$ are expressed in GeV$^2$ in these expressions.
The resonance parameters are indicated in the Table.
| $R$ | | | $m_R$ | $\Gamma_R$ | | | $\phantom{-}$$N_R$ | $\phantom{-}$$\delta_R$ | |
| $a_0(980)$ | | | 0.980 | 0.075 | | | $\phantom{-}$ 1.00 | $\phantom{-}$1.0 | |
| $\pi_1(1600)$ | | | 1.564 | 0.492 | | | $-0.03$ | $-5.0$ | |
| $a_2(1320)$ | | | 1.318 | 0.107 | | | $-0.109$ | $-2.0$ | |
| $a_2(1700)$ | | | 1.722 | 0.247 | | | $-0.036$ | $-2.0$ |
They correspond to the values used in the publication [Mat19a] .
The parameters can be changed in the section Simulation
References
[Mat19a]
V. Mathieu, et al (JPAC),
``Moments of angular distribution and beam asymmetries in $\eta\pi^0$ photoproduction at GlueX,''
arXiv:1906.04841 [hep-ph],
Resources
- C/C++: C/C++ files
- Input file: par_simu.txt , par_model.txt .
- Output files: moment0.txt , moment1.txtt , BA.txt ,
- gnuplot file: gnuplot.txt
- Contact person: Vincent Mathieu
- Last update: September 2019
The file main_GJ.c contains the same function as main.c but rotate the SDME to the GJ frame.
To compile: gcc main.c main_GJ.c modules.c
- par_simu.txt:
The simulation parameters are $E_\gamma$, $t$, $dm$, $isGJ$ - par_model.txt:
The model parameters are $m_R$, $\Gamma_R$, $x_R=1$, $N_r$, $\delta_R$.
The three are lines for the three resonances: $a_0(980)$, $\pi_1(1600)$, $a_2(1320)$. - momentX.txt:
The first column is the $\eta\pi$ mass in GeV. The other columns are $LM=$00, 10,11, 20,21,22, 30,31,32,33, 40,41,42,43,44. - BA.txt:
The first column is the $\eta\pi$ mass in GeV. The second column is the 4 $\pi$ beam asymmetry. The third column is the beam asymmetry along the $y$ axis.
- Moments: Compute the moments $H^{\alpha}(LM)$ from the SDME
- sdme: Compute the SDME $\rho^{\alpha, \ell \ell'}_{mm'}$ from the partial waves.
- partialwaves: Compute the partial waves for our toy model.
- printMoments: Print the moments in files.
- intH and intMoments: integrate the moments in $t$
A general code to reconstruct moments from partial waves is available: C/C++ moments
The zip file contains the files main.cpp, tools.cpp, moments.cpp and their hearders.
The file moments.cpp contains the routines returning all moments for given S, P, D waves (all spin projections).
The file tools.cpp contains the Wigner-d functions and other accessory functions.
The file main.cpp generates random waves and call the moments routines.

